Logic Games Answer
This logic game is a complex relative ordering game. It’s complex because the last two constraints add conditional elements. To fully learn our strategy for this type of game, download the chapter on relative ordering from our book, take our class, or buy our Logic Games book. But for now, let’s use this game as an opportunity to “watch” how Julia, a 170+ LSAT test-taker, approached the game. Keep your conversation to a whisper, turn your cell phone to vibrate, and no flash photography please . . .
Seven dancers -- Mary, Noel, Ophelia, Peter, Rafael, Sue, and Tori -- are preparing to perform a new dance in which the dancers form a straight line facing towards the first and tallest dancer. Each dancer, other than the first, must stand behind a dancer taller than him or herself. No two dancers are of the same height. Every dancer must perform in the dance and no other dancers will participate. The heights of the dancers and their positions conform to the following restrictions:
OK, this is an ordering game – people have to stand in line. Interesting that the tall people are in front – strange dance!
Let me scan the constraints to see if this is relative or numbered. . . OK, this is a relative ordering game – no actual positions are given, just relationships. Time to make a tree.
Mary is taller than Peter and Rafael.
Let’s see which rule I should use next – looks like I’ll skip the next one and use the third, since it mentions Rafael.
Noel is shorter than Ophelia and Sue.
Rafael is taller than Noel but shorter than Tori.
Mary is taller than Peter and Rafael.
Let’s see which rule I should use next – looks like I’ll skip the next one and use the third, since it mentions Rafael.
Noel is shorter than Ophelia and Sue.
Rafael is taller than Noel but shorter than Tori.
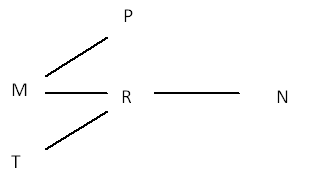
Now I can use the second one, since I have Noel in the diagram at this point. Here’s what I have so far:
Noel is shorter than Ophelia and Sue.
Rafael is taller than Noel but shorter than Tori.
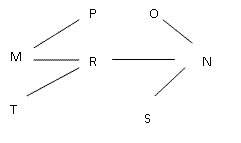
Let me make sure I arranged these in the right order . . . quick scan of the constraints -- did I consistently put taller dancers to the left side? Looks good. Now on to the last two constraints.
If Mary dances next to Tori, then Ophelia dances immediately in front of Sue.
If Tori does not dance next to Mary, Ophelia dances immediately in front of Noel.
Hmm, these are tricky -- let me write these out.

I’ll write MT/TM to show that either can come first, and drawing a line through it means that it does not occur.
These constraints are tricky! I bet some questions will hinge on them. Let’s think about it for a second. Well, we either will have M and T next to each other or not, so either the line–up will include ON or OS.
This is a strange tree! Let me orient myself before beginning. I’ll write out one option: M T P R O S N. OK, let’s go!
(A) Mary, Peter, Tori, Rafael, Sue, Noel, Ophelia
(B) Tori, Sue, Mary, Rafael, Ophelia, Noel, Peter
(C) Ophelia, Tori, Mary, Rafael, Sue, Peter, Noel
(D) Sue, Tori, Ophelia, Mary, Peter, Rafael, Noel
(E) Noel, Sue, Ophelia, Rafael, Peter, Mary, Tori
This is an orientation question -- let me use my tree to answer this.

I can use the string MRN to see which choices I can eliminate. Let’s see. . . That eliminates (E).
How about MP? . . . That doesn’t eliminate anything. There aren’t many long chains, so let me use the tricky constraints, they’ll probably eliminate a few choices.

If MT/TM . . .that’s in (C), so is OS there? No, so (C) is out.
If M is not next to T, that’s in (A), and is ON there? No, so (A) is out.
(B) has M and T separate, and ON is there, so keep it.
(D) has M and T separate, and no ON, so (D) is out. That leaves me with (B).
(A) Sue dances someplace behind Noel.
(B) Peter dances immediately behind or immediately in front of Ophelia.
(C) Mary dances either first or second in the line.
(D) Tori dances someplace before Peter.
(E) Ophelia does not dance immediately in front of or immediately behind Sue.
Alright, they have given me a position, let me write this out:
____ ____ ____ ____ ____ _R___ ____
So, following the inference chain, this means that N must be last
____ ____ ____ ____ ____ __R__ __N__
And let’s see, that means that ON can’t occur, since N is stuck behind R. That means that M and T must be adjacent to one another. What about the other elements are there any positions that are required or not allowed . . . I’m not sure. Maybe this is an easy question and the answer simply hinges on N being last. (A) mentions N, but it has S dancing behind it --d that can’t be true, (A) is out. Well, that’s if for the N rule.
Hmmm, let me write out a quick possible arrangement and see if it provides scenarios that contradict answer choices and therefore helps me eliminate them since they must be true : T M O S P R N
(B) can be eliminate since in my example, P and O are not adjacent.
(C) looks good, keep it.
(D) is also true in my scenario, keep it.
(E) is fishy . . . yes, it is not true here, O can dance next to S, so (E) is out.
So I’m left with (C) and (D), let’s look.
With (C), can we put M somewhere other than first or second? Who has to come after it? I guess just R and N, oh wait, and P. It seems like there isn’t enough room for all of those. So that seems like it’s not the answer, but I’m not 100%, let me check (D). Can T come after P? . . . No, it can’t since MT have to be adjacent and P follows M, it can’t squeeze between them, and so must also follow T. (D) is it!
3. Which one of the following must be false?
(A) Peter dances second and Noel dances sixth.
(B) Tori dances fourth and Ophelia dances sixth.
(C) Mary dances first and Peter dances seventh.
(D) Ophelia dances third and Sue dances fourth.
(E) Rafael dances sixth and Noel dances seventh.
Wow, this game has a lot of tough questions! Must be false . . . hmm, not much to go on here. Let’s start cranking through the answer.
(A)
____ __P___ ____ _____ _____ ____ __N___
Hmm, if N is last, who goes after it? Can’t be O, S, R . . . wait, it must be P. Ahh! This must be false. No need to check the others (and no time!).
4. If Tori dances second, which one of the following is a complete and accurate list of all the positions in which Rafael could dance?(A) third, fourth
(B) fifth, sixth
(C) third, fifth, sixth, seventh
(D) fourth, fifth, sixth
(E) third, fourth, fifth, sixth
OK, let’s draw this out too.
____ __T___ ____ _____ _____ ____ _____
OK, where can R go? Let’s see, it must come afterwards. What about at the end of the line-up? N has to come after R, so that takes out the seventh position and answer (C). Hmm . . . well, R could go third, with M in slot one and then OS in the fourth and fifth positions, with P and N down the line, like this:
_M___ __T___ __R__ __O___ __S___ _P___ __N___
So (B) and (D) are out. Let’s see what’s left. The difference between (A) and (E) is whether fifth and sixth are OK. So let’s check sixth.
____ __T___ ____ _____ _____ __R__ _____
We’d have to put N last, which means we have to have OS, which means M/T, so M could be first, P could be third, OS fourth and fifth. Yeah, that’s OK. Alright, that seems fine, so (E) is the answer.
Notice how this test-taker was very flexible in her approach. Some important moves that you might have glossed over:
• Writing out one scenario before diving into the question if the game seems opaque. This is a questionable move in that it can lead to time-consuming trial and error, but if you feel that you don’t have a handle on a game and if you can do it quickly, the comfort may be worth the 10 seconds.
• In question 1, she used the diagram to eliminate answers on the orientation question (the first one). While the constraints are written immediately above the first question, using the diagram strengthens your grasp of its meaning.
• In questions 2 - 4, she wrote out a number line since each question defines a position for an element. Then she followed the inference chain to see what can be concluded from that.
• When solving question 2, she “kept” answers while going on to evaluate others. Ideally you can eliminate answers as you go, but with wide open questions, you sometimes have to withhold judgments while you look for answers that are easily eliminated. It’s often easier to eliminate four answers than to find the one right one.
• Question 4 could have been difficult, but once our test taker found the right answer, she moved on. There’s no time to evaluate after such a definitive moment!
• For the last question, after eliminating three answers, it was useful to compare the remaining answers to see what should be evaluated to choose between those two. For example, it would have been pointless to test out whether R could have been fourth, since both answers included that.
In case you missed it, the correct answers were B, D, A and E. If you have any questions, e-mail logicmaster@manhattanlsat.com.