GRE Math for People Who Hate Math: Remainder Problems
You can attend the first session of any of our online or in-person GRE courses absolutely free. Crazy, right? Check out our upcoming courses here.
The secret to understanding GRE remainder problems is in the word remainder itself. Suppose you bake a dozen brownies, and while you’re at work, your roommate eats ten of them. The two brownies left over are the remainder of the batch. The mathematical term remainder refers to the same thing: what’s left over after something is taken away.
Here are those brownies again:
And here’s a piece of a GRE Quant problem:
What is the remainder when 12 is divided by 5?
The word “divided” in there makes you want to start doing division. But if you divide 12 by 5, you end up with 2.4. So what? That 2.4 won’t help you answer the question you’re being asked.
When you first learned about division as a kid, you may have learned that dividing is the same as splitting a larger group up into smaller groups. When you divided 12 by 5, you learned to picture twelve brownies being split into groups of 5 brownies each.
You didn’t even know about decimals yet, so you didn’t know that the real answer was 2.4. You did know that there were two full groups, so the answer was bigger than 2 but smaller than 3. You also knew that there were two brownies left over. Those two brownies were the remainder.
This might seem like kid stuff—and that’s because it is! In order to handle remainder problems, you want to think about division in a less sophisticated way than you’re used to. Imagine splitting a large number of brownies into smaller groups of a certain size. When you can’t make any more groups, you’re finished. Look at the extra brownies that are left over: that’s your remainder.
Bonus question for GRE Quant gurus: On the GRE, it’s useful to know that the remainder is always smaller than the number you’re dividing by. For instance, if you divide 43,894,784,412 by 7, the remainder will definitely be smaller than 7. Why is that true?
Suppose that instead of a dozen brownies, we had exactly 503 brownies. (Too many brownies? Nah.)
And let’s suppose that instead of dividing by 5, we’re dividing by 7. Now we’ve got a GRE problem that looks like this:
What is the remainder when 503 is divided by 7?
If you had a ridiculous amount of time on your hands, you could start splitting the 503 brownies into groups of 7, one group at a time. When you finished, you could check how many brownies were left over. That number would be the remainder.
Let’s take a shortcut, though. Instead of counting one group at a time, let’s count ten groups at a time. In other words, we’re going to remove 70 brownies at once, not just 7.
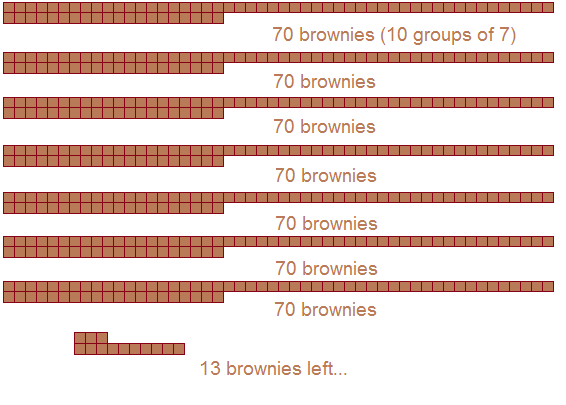
We’ve got 13 brownies left over. That doesn’t mean the remainder is 13, though. We could actually remove one last group of 7, leaving us with just 6 brownies:
The remainder when we divide 503 by 7 is 6.
We need a way to take this shortcut without visualizing brownies (as fun as that is). Here it is. We wanted to find the remainder when we divided 503 by 7. In order to do so, think of a number smaller than 503 that can be divided evenly into groups of 7. For instance, we might think of 490, because 490 = 70 x 7. We can remove the first 490 brownies, and we’re left with 503 — 490 = 13.
Then, if necessary, repeat the process: think of a number smaller than 13 that can be divided evenly into groups of 7. Here, the only number that works is 7. Remove the next 7 brownies, and you’re left with 6.
Try it on this problem:
What is the remainder when you divide 77,218 by 7?
Here’s my approach. 77,000 is divisible by 7. So, I can subtract it right away. Now, I’m only looking for the remainder when 218 is divided by 7. I know that 210 is divisible by 7, so I’ll subtract that as well: 218 – 210 = 8. 8 isn’t the remainder, though. I can still remove one final group of 7 brownies, leaving me with exactly 1 left over. The remainder is 1.
Bonus question for GRE Quant gurus: Suppose that the remainder when x is divided by 7 is 4. What’s the remainder when x + 14 is divided by 7? How about when x + 100 is divided by 7?
Finally, let’s go in the opposite direction. In the problems above, you needed to find the remainder. What if you already knew the remainder? Suppose that I told you that I baked a certain number of brownies—at least 10 of them. When I divided those brownies into groups of 10, I ended up with 2 left over. What do you know about how many brownies I have?
In other words,
The remainder when x is divided by 10 is 2.
Let’s start by finding the smallest number of brownies I might have had. I already told you that I removed groups of 10 brownies and had 2 left over. What if I only removed one group of 10?
Then you know that I started with 10 + 2, or 12.
What if I removed two groups of 10?
Then you know that I started with 2 x 10 + 2, or 22.
What if I removed three groups of 10? Then I must have started with 3 x 10 + 2, or 32.
That’s how you list all of the numbers with a certain remainder! Start with the number you would have had if you removed one group. That will be the sum of the remainder and the number you’re dividing by. Here, that was 12. Then, find the next largest value. Here, since we’re removing groups of size 10, we’ll have to count up by 10s. The possible values for x were 12, 22, 32, 42, 52… on up to infinity.
Let’s try one final GRE remainder problem to wrap things up:
The integer x is between 50 and 60, inclusive. The remainder when x is divided by 7 is 3. What is the sum of all possible values of x?
The remainder when x is divided by 7 is 3. That means that when we removed groups of 7 brownies, we ended up with 3 brownies left over. The smallest possible number that works would be 10 brownies. That’s too small, though, since it isn’t between 50 and 60! Count up by 7s to find other numbers that could work: 10, 17, 24, 31, 38, 45, 52, 59, 66. The only two values in the range are 52 and 59. The problem asks for their sum, so plug those numbers into your calculator (or use some of the mental math magic you learned from Neil): the answer is 111. ?
See that “SUBSCRIBE” button in the top right corner? Click on it to receive all our GRE blog updates straight to your inbox!
Chelsey Cooley
is a Manhattan Prep instructor based in Seattle, Washington. Chelsey always followed her heart when it came to her education. Luckily, her heart led her straight to the perfect background for GMAT and GRE teaching: she has undergraduate degrees in mathematics and history, a master’s degree in linguistics, a 790 on the GMAT, and a perfect 170Q/170V on the GRE. Check out Chelsey’s upcoming GRE prep offerings here.