More GRE Math Misconceptions
Did you enjoy our last set of GRE Math Misconceptions? Here are four more to watch out for.
Mistake: If you raise a negative number to a negative exponent, the answer will definitely be negative.
Fact: Weirdly enough, a negative number with a negative exponent can come out positive. Check out this expression:
To simplify it, remember that a negative exponent is “shorthand” for an exponent in the bottom of a fraction. This is what the expression really means:
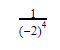
What happens when you raise -2 to the 4th power?
The answer comes out positive.
Why?: All that matters is whether the exponent is even or odd. If the exponent is even, the result will always be positive. That’s true even if the exponent is a negative even number. When you see a negative number and a negative exponent, don’t automatically assume that the answer will be negative too. Check whether the exponent is odd or even first.
Mistake: -1/3 is smaller than -1/2.
Fact: -1/3 is actually greater than -1/2.
Why?: Draw a number line:
On a number line, numbers to the left are always smaller than numbers to the right. Counterintuitively, since -1/2 is to the left of -1/3, -1/2 is smaller. (A quick way to check this is to decide which one should be further away from zero.) So, if you’re writing an inequality, it should look like this:
This is a good example of something that might seem clear now, but that can easily trick you if you’re working quickly. If you’re comparing negative numbers on the GRE, especially negative fractions, consider drawing a quick number line. At the very least, slow down for a moment!
Mistake: There are 12 numbers between 8 and 20, inclusive. (By the way, ‘inclusive’ just means ‘including the numbers at the ends,’ which are 8 and 20 themselves.)
Fact: There are actually 13 numbers in that range. To be completely certain, count them:
8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Why?: The issue arises when you just subtract 8 from 20 and get 12. Just subtracting doesn’t give you the right number of terms. You need to add 1 to whatever you got.
To see why this happens, go back to the number line. Place a token on every integer from 1 to 20:
When you subtract 8 from 20, that’s the equivalent of removing the first 8 tokens:
When you do that, though, you don’t have tokens on the numbers from 8 to 20, inclusive! You’re actually missing one token: the one that’s supposed to be on 8. That’s why your result will turn out 1 too low. When you subtracted, you ‘removed’ one too many tokens.
Mistake: To find the solution to this equation:
x (3x – 1) = 8x
Start by dividing both sides of the equation by x.
Fact: Hold on! The equation actually has two solutions: x = 3, and x = 0. But if you start by dividing both sides by x, you only find the first solution. That could cause you to miss the right answer.
Why?: On the GRE, you’re never allowed to divide by 0. Since x is a variable, you don’t know what it equals: it could be 5, 100, -3, or even 0. If you divide by x, you could be dividing by 0 accidentally. That’s an ‘illegal move’ and will cause your math to come out wrong.
To avoid accidentally dividing by 0, don’t divide both sides of an equation by a variable unless you’re sure it doesn’t equal 0. Instead, simplify using addition, subtraction, and multiplication:
x (3x – 1) = 8x
3x² – x = 8x
3x² – 9x = 0
x (3x – 9) = 0
Now, either x equals 0, or 3x – 9 equals 0 (in which case x is 3). ?
See that “SUBSCRIBE” button in the top right corner? Click on it to receive all our GRE blog updates straight to your inbox!
Chelsey Cooley
is a Manhattan Prep instructor based in Seattle, Washington. Chelsey always followed her heart when it came to her education. Luckily, her heart led her straight to the perfect background for GMAT and GRE teaching: she has undergraduate degrees in mathematics and history, a master’s degree in linguistics, a 790 on the GMAT, and a perfect 170Q/170V on the GRE. Check out Chelsey’s upcoming GRE prep offerings here.