GRE Quantitative Comparisons: The Equal-Different Method
You can attend the first session of any of our online or in-person GRE courses absolutely free. Ready to take the plunge? Check out our upcoming courses here.
There are many different approaches to tackling GRE Quantitative Comparisons problems. One of my favorites is something that, in my opinion, generally doesn’t get talked about enough. This method is for people who feel very comfortable with the basics of quantitative comparisons, and have a decent handle on mental math. When executed properly, it can save you a great amount of time on the test, thus giving you the opportunity to solve other problems. It also can help avoid making silly errors by reducing the number of paper-and-pencil calculations you have to do. This method is called the Equal-Different, or E-D, method.
The method is a variant of “Proving D”. Let’s refresh our memories on that, then we’ll move on to discussing the E-D method.
The basic idea of proving D, in GRE Quantitative Comparisons, is to plug in different numbers for the variables in the problem and see if you get different results. Consider the following problem:
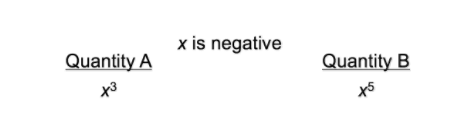
To solve the problem using the “Prove D” method, we would plug in different values of x and see if we get different results. For instance, we might start by plugging in the value of -2. If we plug in -2 for x, Quantity A is -8 and Quantity B is -32. Quantity A is bigger.
Then we would look for a another value of x that gives us a different result. We might pick the value -½. If we plug in -½ for x, then Quantity A is -1/8 and Quantity B is -1/32. In this case, Quantity B is bigger. (Remember, with negative numbers, a quantity is bigger if it is further to the right, or closer to zero, on the number line. -1/32 is closer to 0 than -1/8, so it is bigger!) Because Quantity A is bigger in our first example, and Quantity B is bigger in our second example, we would be justified in choosing D.
The E-D method is a lot like this! But it’s a little scrappier and involves fewer steps. It involves less calculator work and a bit more mental math. As a result, it can save you some important seconds on the test—provided you do it right!
The crux of the E-D method relies on two questions:
1. Can I get the quantities equal to each other?
2. Can I get the quantities different from each other?
To see how these questions play out, let’s apply them to the problem. Let’s first ask ourselves whether we can pick values of x that will make the quantities equal. Figured it out? If you said -1, you’re right. Plugging in -1 for x will make Quantity A equal to Quantity B.
Great! Now all that’s left is question 2: can I make them different? But this is the easy part. A quick glance at the problem will tell you that any other value of x will cause the quantities to diverge.
What does this mean? Well, it means you’ve just proven D in a scrappy way: if the quantities can be equal sometimes, but could also be different sometimes, then the answer must be D.
Congratulations! You have just completed your first GRE Quantitative Comparisons problem using the E-D method. Let’s try another one to make sure you’ve got the hang of it. Consider the following:
Now, this is another situation in which you could use the traditional “Prove D” method to solve the problem. That would involve selecting a set of numbers for a and b, plugging them in, obtaining the result, selecting a second set of numbers for a and b, plugging them in, and finally comparing your first and second result. Furthermore, if you happen to get the same result, then you ought to try a third set of numbers to make sure you’ve got it right!
But you’re smarter than that. You recognize that, in a problem like this, it’s going to be best to use the E-D method. Let’s try.
First, ask yourself: Can I find values of a and b that will make the quantities equal?
If you came up with the number “1” for both a and b, you’re right. This number would produce the same value for both quantities. In fact, you may notice that, as long as b is set to 1, then it doesn’t matter what a is! The quantities will always be the same. (Setting a to 0 will also produce equivalent values.)
Now, onto the second question: Can I find values that will make them different? This should be the easy part! Plug in almost any value for b other than 0 and 1 and you will produce different values for the quantities. Presto! You have just proven D using the E-D method.
Keep an eye out for problems like this! When they arise, you will find that the E-D method gives you a quick, efficient, mental shortcut for proving D that doesn’t rely on a series of plugged-in numbers.
Of course, not every GRE Quantitative Comparisons problem will be conducive to this method. Typically, appropriate problems are ones that contain variables in the quantities and lend themselves to having 0’s and 1’s plugged into them, including problems with exponents, fractions, and negatives/positives.
Overall, you are likely to find at least a handful of problems like this on the GRE. So make sure to keep this method in mind, and practice it when you can!
Want more guidance from our GRE gurus? You can attend the first session of any of our online or in-person GRE courses absolutely free! We’re not kidding. Check out our upcoming courses here.
Daniel Yudkin
is a Manhattan Prep instructor based in New York, NY. He has been a test prep instructor for over seven years and is currently in the final stage of a Ph.D. program in social psychology at NYU. In his spare time, Daniel writes popular science articles about psychological phenomena and is a devoted jazz pianist and vocalist. Check out Daniel’s upcoming GRE prep offerings here.