Let’s Have Fun with GRE Exponents
 You may already know the basic rules of exponents for the GRE. These rules tell you what to do if you want to multiply or divide two exponential numbers, or raise an exponent to another power. Once you’ve memorized them, exponent problems become exponentially easier (I’m so sorry). But there are two types of exponent problems that many students find intimidating, because the basic rules just don’t seem useful. In this article, we’ll go over those two problem types, how to recognize them, and what to do if you see one.
You may already know the basic rules of exponents for the GRE. These rules tell you what to do if you want to multiply or divide two exponential numbers, or raise an exponent to another power. Once you’ve memorized them, exponent problems become exponentially easier (I’m so sorry). But there are two types of exponent problems that many students find intimidating, because the basic rules just don’t seem useful. In this article, we’ll go over those two problem types, how to recognize them, and what to do if you see one.
Adding and subtracting exponents
Here’s a problem from the Exponents and Roots chapter of the GRE 5lb. Book:

Look at the numerator of that fraction. There isn’t an ‘exponent rule’ for handling subtraction, or addition, between two exponential numbers. It’s also impossible to calculate the value of the numerator on paper, since the numbers are much too big. Nonetheless, you can simplify it by factoring out the greatest common factor.
Both 4050 and 4048 are divisible by 4048. Factoring out a 4048 term from the numerator gives the following:

From here, the problem can be simplified using only the usual exponent rules. I’ll leave that to you! But here’s the rule to remember, since it allowed us to take the first step towards simplifying this problem: when you see two exponential values with the same base being added or subtracted, find the largest common term and factor it out.
Test that skill by simplifying the following:
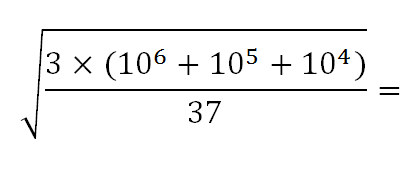
Sneaky special quadratics
When is an exponent problem not an exponent problem? When it’s a quadratic problem in disguise. Here’s one more problem from the GRE 5lb. Book:
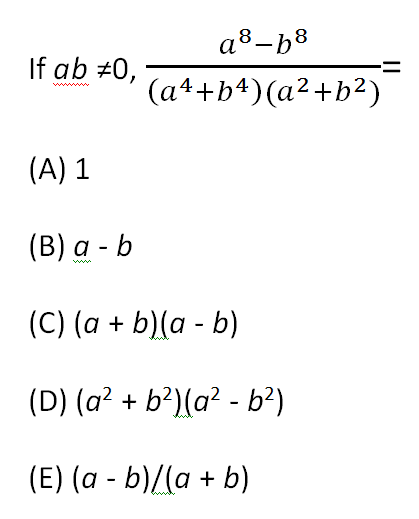
The numerator looks similar to the ones in the previous two problems, but this time, the bases of the two exponential numbers are different. You can’t factor out a common term unless you know the values of a and b. What you can do, though, is recognize the numerator as a difference of squares.

Both a8 and b8 are perfect squares. Specifically, they’re the squares of a4 and b4, respectively. Their difference can be simplified using the difference of squares formula, x2 – y2 = (x – y)(x + y). This is true whenever a number has an even exponent. So if you see a difference of exponential numbers, and both exponents are even, consider simplifying in this way. In this case, the expression can even be simplified further, since both a4 and b4 are perfect squares:

Finally, simplify the entire fraction:

The correct answer is (C) (a + b)(a – b), which is equal to a2 – b2 .
Try simplifying one more expression for practice. This time, you’ll need both of the skills discussed in this article:

When you see something in an exponent problem that doesn’t fit the rules, ask yourself if it’s one of these two special exponent problem types. It may require you to factor out a common term, require you to use the difference of squares rule, or possibly both. If so, don’t get intimidated! Just follow those rules and keep simplifying. 📝
Chelsey Cooley is a Manhattan Prep instructor based in Seattle, Washington. Chelsey always followed her heart when it came to her education. Luckily, her heart led her straight to the perfect background for GMAT and GRE teaching: she has undergraduate degrees in mathematics and history, a master’s degree in linguistics, a 790 on the GMAT, and a perfect 170/170 on the GRE. Check out Chelsey’s upcoming GRE prep offerings here.
is a Manhattan Prep instructor based in Seattle, Washington. Chelsey always followed her heart when it came to her education. Luckily, her heart led her straight to the perfect background for GMAT and GRE teaching: she has undergraduate degrees in mathematics and history, a master’s degree in linguistics, a 790 on the GMAT, and a perfect 170/170 on the GRE. Check out Chelsey’s upcoming GRE prep offerings here.
Your comment is awaiting approval.