Remainders – Who Needs Them Anyway??
 We were taught in school to think of whole numbers in the context of two groups: Odds vs. Evens. I remember thinking it was like the black vs. white pieces on a chess board (I was kind of a nerd). As I’m sure you know, an Even number is simply a number divisible by 2, and an Odd number is any number that’s not even. But ask yourself this: what is the remainder when you divide an odd number by 2? Take a minute to think about this. Try out a few different odd numbers and see if you can identify a pattern.
We were taught in school to think of whole numbers in the context of two groups: Odds vs. Evens. I remember thinking it was like the black vs. white pieces on a chess board (I was kind of a nerd). As I’m sure you know, an Even number is simply a number divisible by 2, and an Odd number is any number that’s not even. But ask yourself this: what is the remainder when you divide an odd number by 2? Take a minute to think about this. Try out a few different odd numbers and see if you can identify a pattern.
The remainder will always be 1 when you divide an odd number by 2. Always. And when you divide an even number by 2? Well, by definition the even number is divisible by 2, so the remainder is therefore zero.
The GMAT loves taking this concept and testing how deep your understanding goes. Therefore, we must free ourselves of the simplistic odd vs. even framework that we were fed in school, and explore this concept to a much deeper level. That is exactly what I intend to do in this blog post.
I always joke with my students that if I were the number 3 on the number line, I would really hate my next door neighbor to the left (number 2). He thinks he’s so special because there’s a name for any multiple of him (“even”); and if that’s not enough to give him a big head, they also invented a name for any number that isn’t a multiple of him (“odd”). What do you call multiples of me? “multiple of 3”. What do you call numbers that are not multiples of me? “not a multiple of 3”. LAME
Another Way To Solve Median & Mean Questions
 This is the second of a series of posts that offer alternate ways to solve certain GMAT problems (check out the first here: DS Value Problems). Just like last time, if you like the method, steal it! And if you don’t, I promise not to lose any sleep. There’s a lot of ways to solve most questions on the GMAT and the best way will always be the way that works best for you. So without further ado, let’s check out a GMATPrep question and see how fast you can solve:
This is the second of a series of posts that offer alternate ways to solve certain GMAT problems (check out the first here: DS Value Problems). Just like last time, if you like the method, steal it! And if you don’t, I promise not to lose any sleep. There’s a lot of ways to solve most questions on the GMAT and the best way will always be the way that works best for you. So without further ado, let’s check out a GMATPrep question and see how fast you can solve:
Last month 15 homes were sold in Town X. The average (arithmetic mean) sale price of the homes was $150,000 and the median sale price was $130,000. Which of the following statements must be true?
I. At least one of the homes was sold for more than $165,000.
II. At least one of the homes was sold for more than $130,000 and less than $150,000.
III. At least one of the homes was sold for less than $130,000.
(A) I only
(B) II only
(C) III only
(D) I and II
(E) I and III
First things first, if you answered this question using algebra, you’re in great company. Another one of our instructors, Stacey Koprince, has a great write up on the algebra in this question, and it’s definitely worth a read-through right here. But a lot of questions on the GMAT, including this one, can be solved by thinking of extremely simple scenarios, rather than the algebra that determines all of them.
The first thing I noticed on this question is that this is one of those awful questions where there’s a whole lot of wiggle room with the information that they give you. What was the cheapest house? What was the cost of the third most expensive house? Were any of the houses all the same price? If the second cheapest house is half as expensive as the most expensive, how does that affect the cost of the other houses? It’s easy to get lost when you start to think about how little you know in this scenario.
But before I jump around and start picking values out of thin air, the most important part of this problem are the (few) things that MUST be true. In this case, there are two: the 15 house prices have a mean of $150,000 and a median of $130,000. And on my paper, I would write out a few slots to represent the house prices like this: (note- I wouldn’t write out all 15 slots. Just the first few, the last few, and, since this is a median problem, one in the middle.)
|
____ |
____ |
… |
____ |
… |
____ |
____ |
|
1 |
2 |
7 |
14 |
15 |
Again, there are two things that they tell me here, but I want to start with the most restrictive element in this problem. There are lots of different ways to get a mean of $150,000, but in order to get a median of $130,000, I would need at least one house to cost EXACTLY $130,000. So I add that to my chart (ignoring the $ sign and extra zeroes):
GMAT Challenge Problem Showdown: July 15, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
If n is a positive integer greater than 1, what is the smallest positive difference between two different factors of n?
(1)
is a positive integer.
(2) n is a multiple of both 11 and 9.
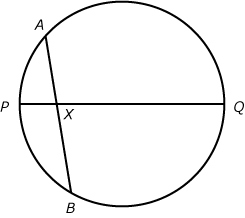
GMAT Challenge Problem Showdown: July 8, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
If PQ is a diameter of the circle above, and the lengths of AX, BX, PX, and QX are integers, what is the area of the circle?(1) (AX)(BX) = 16
(2) QX > AB
GMAT Challenge Problem Showdown: July 1, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
You have 1 minute (yes, only one minute!) to do this problem. Further, don’t do any long-hand math (multiplication, etc.)”shortcuts exist for every single calculation. Find them!
In how many ways can a four-letter password be chosen, using the letters A, B, C, D, E, and/or F, such that at least one letter is repeated within the password?
GMAT Challenge Problem Showdown: June 24, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
A point Q is located within the interior of a square ABCD so that it is 1 unit from vertex A, 2 units from vertex B, and 3 units from vertex D. The measure of angle AQB is
Giveaway Data Sufficiency Statements
 Data sufficiency question are a strange animal that exists only in GMAT land. The newness of this question type creates high levels of anxiety because we don’t know how to react when we see something new (How do you think you would react if you were standing face to face with a unicorn?). Once we get over this newness, data sufficiency questions all follow a specific morphology, and in my opinion actually contain less diversity than problem solving questions. There is always either a yes/no question (is ab even?) or value question (how many boys are in the class?), followed by two statements, and the five answer choice are always the same and in the same order. (If you are completely unfamiliar with data sufficiency questions take a look at an example here)
Data sufficiency question are a strange animal that exists only in GMAT land. The newness of this question type creates high levels of anxiety because we don’t know how to react when we see something new (How do you think you would react if you were standing face to face with a unicorn?). Once we get over this newness, data sufficiency questions all follow a specific morphology, and in my opinion actually contain less diversity than problem solving questions. There is always either a yes/no question (is ab even?) or value question (how many boys are in the class?), followed by two statements, and the five answer choice are always the same and in the same order. (If you are completely unfamiliar with data sufficiency questions take a look at an example here)
Because of this very confined structure, there are actually cases where the structure of question and statements can give you information regardless of the specifics of the problem. There are at least four instances where a specific form of the statement(s) will allow you to eliminate several responses without evaluating the full content of the problem.
1) A value statement for a yes/no question
If a statement provides a value for the sole variable in the question, it is definitely sufficient to answer any yes or no question.
For example:
GMAT Challenge Problem Showdown: June 17, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:

Triangle ABC is cut by a line DE parallel to side AC, as shown in the diagram. If side AC has length 1, and the area and perimeter of triangle ABC are both twice the corresponding values for trapezoid ADEC, what is the perimeter of triangle DBE?
GMAT Challenge Problem Showdown: June 10, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
Each of seven consecutive integers, all greater than positive integer n, is divided by n. The seven resulting remainders, not necessarily distinct, are assembled into a list L. What is the value of n?
(1) List L contains two odd values and 5 even values.
(2) No odd integer appears in list L more than once.
GMAT Challenge Problem Showdown: June 3, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
An insect is located at one corner (point A) on the surface of a rectangular solid that measures 3 x 4 x 5 inches, as shown in the diagram.
Note: Figure is not drawn to scale.If the insect crawls along the surface of the rectangular solid to the opposite corner (point B), what is the shortest possible length, in inches, of the insect’s path from point A to point B?
 is a positive integer.
is a positive integer.